Расчет кроссовера для акустики расчет кроссовера для акустики

Проектирование и расчёт пассивных разделительных LC фильтров
(кроссоверов) для акустических систем

Онлайн калькулятор акустических фильтров 1. 6-го порядков: нижних частот (ФНЧ) для
низкочастотных динамиков, фильтров верхних частот (ФВЧ) – для высокочастотных,
а также полосовых фильтров (ПФ) – для среднечастотных.
Расчёт согласующей цепи Цобеля и Г- образного аттенюатора для громкоговорителя.

В настоящее время практически все качественные акустические системы являются многополосными, т. е. состоящими из нескольких громкоговорителей, каждый из которых работает в своём, отведённом ему диапазоне частот. Для распределения энергии звукового сигнала между динамиками используют электрические разделительные фильтры (КРОССОВЕРЫ), в данном рассматриваемом случае — пассивные LC-фильтры, которые включаются между выходным разъёмом усилителя, обладающего близким к нулю выходным сопротивлением, и динамической головкой АС.
Надо отметить, что данные разделительные фильтры являются одним из важнейших компонентов акустических систем, определяя весомую часть необходимых электроакустических характеристик, а также качества и естественности звучания тракта.

Сколько полос иметь? На каких частотах делить звуковой частотный диапазон? Какого типа и какого порядка использовать разделительные фильтры в кроссоверах, а также — какими эти фильтры будут обладать характеристиками — вот вопросы, которые устойчиво стоят на повестке дня и требуют аккуратного и подробного обсуждения.

Часть ответов на эти вопросы можно найти в довольно показательной таблице сравнительных характеристик различных фильтров, опубликованной в журнале «Автозвук», № 5/2001.
Таблица примечательна тем, что в ней приведены только реально применяемые кроссоверы без упоминания редко используемых типов фильтров, а также фильтров с нежелательными для акустики свойствами.

Краткая сравнительная характеристика разделительных фильтров акустических систем

Главным достоинством фильтров первого порядка является возможность одновременного достижения идеальной (плоской) АЧХ и идеальной (нулевой) ФЧХ. Недостаток фильтров первого порядка – слабые фильтрующие свойства

Любой фильтр второго, шестого, десятого и т.д. порядка обладает недостатком: при отсутствии переполюсовки динамиков АЧХ имеет провал, при переполюсовке возможны проблемы с импульсным откликом

Хороший фильтр с хорошим звуком. Отличные импульсные характеристики. Как правило, требует переполюсовки одной из головок

Обеспечивает гладкую АЧХ при очень хороших ФЧХ и импульсных характеристиках

Дает выброс 3 дБ на частоте раздела. Один из способов борьбы с выбросом – разнесение частот среза ФНЧ и ФВЧ

Фильтры третьего порядка обеспечивают достаточно высокую степень разделения при все ещё приемлемых ФЧХ и ГВЗ. Наиболее перспективны в большинстве устройств. Переполюсовка одной из головок приводит к иным последствиям, чем у фильтров 2-го порядка: АЧХ не меняется, характер ГВЗ улучшается, звук – дело вкуса

Имеет небольшое отклонение АЧХ от идеала в районе частоты раздела. Обладает улучшенными импульсными характеристиками

Применяется редко

Является основным среди фильтров третьего порядка, так как единственный обеспечивает плоскую АЧХ

Фильтры четвертого порядка применяются только в специальных случаях, когда по каким-то причинам требуется очень жесткое частотное разделение. ФЧХ и импульсные характеристики на грани допустимого. В отличие от фильтров второго порядка – не требуют переполюсовки

Практически не имеет отличий от фильтра Линквица – Райли

Обладает гладкой АЧХ

Используется редко

Используются чрезвычайно редко, например, при необходимости очень резкого ограничения полосы частот, подаваемых на низкочастотный динамик или сабвуфер. Переполюсовка просто вредна

Применяется редко

Применяется редко

Обладает гладкой АЧХ

Порядок фильтра	Бесселя	Линквица – Райли	Баттерворта
1
3
4
5

От себя добавлю, что действительно — фильтры 5-го порядка используются редко, однако если требуется существенное подавление внеполосных частот, подаваемых на сабвуфер, то в качестве ФНЧ, как правило, применяются фильтры не 5-го, а 6-го порядков и не Баттерворта, а Линквица – Райли.
Приведём схемы LC фильтров верхних и нижних частот 6-го порядка. Схемы фильтров меньших порядков образуются путём отбрасывания соответствующих элементов (Рис.1).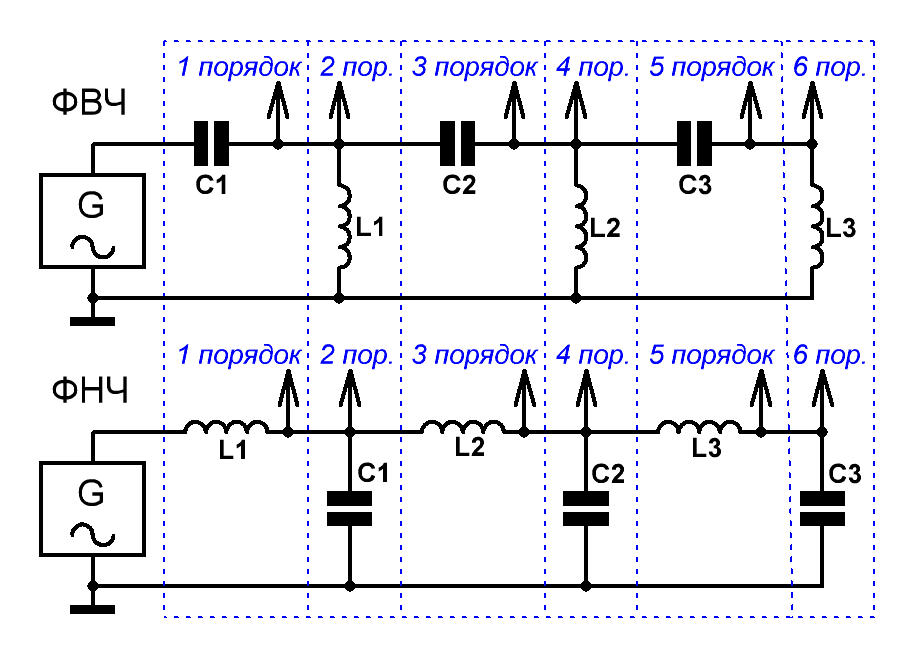

Рис.1 Схемы односторонне нагруженных LC фильтров верхних и нижних частот

Для фильтров нижних частот — значения величин элементов, соответствующих: порядку фильтра, сопротивлению нагрузки Rн и частоте среза (разделения) Fср, рассчитываются по следующим формулам:
L_i= α_i*R_н/(2πF_ср) ; C_i= α_i/(2πF_ср*R_н) , где α_i — это справочные нормированные значения (коэффициенты) для каждого элемента ФНЧ, называемые значениями элементов фильтра-прототипа.

Для фильтров верхних частот — каждая индуктивность из схемы ФНЧ заменяется ёмкостью, ёмкость — индуктивностью, которые, исходя из тех же самых коэффициентов, рассчитываются по формулам:
C_i= 1/(2πF_ср*α_i*R_н) ; L_i= R_н/(2πF_ср*α_i) .

Оставим все многочисленные таблицы со значениями нормированных коэффициентов фильтров-прототипов для справочной литературы, а сами сразу перейдём к онлайн расчёту номиналов элементов кроссоверов.

КАЛЬКУЛЯТОР РАСЧЁТА ЭЛЕМЕНТОВ ФНЧ и ФВЧ LC- ФИЛЬТРОВ ДЛЯ АКУСТИЧЕСКИХ СИСТЕМ

Для полосовых фильтров: каждый элемент-индуктивность из НЧ фильтра-прототипа заменяется на последовательный LC контур (Рис.2), элементы которого рассчитываются по следующим формулам:
L_i= α_i*R_н/[2π(F_в — F_н)] , где Fн и Fв – нижняя и верхняя частоты среза полосового фильтра, а
C_i= 1/(4π 2 *F_н*F_в*L_i) .
Каждый элемент-ёмкость из фильтра-прототипа нижних частот заменяется на параллельный LC контур, элементы которого рассчитываются по формулам:
C_i= α_i/[2π*R_н*(F_в — F_н)] ;
L_i= 1/(4π 2 *F_н*F_в*C_i) .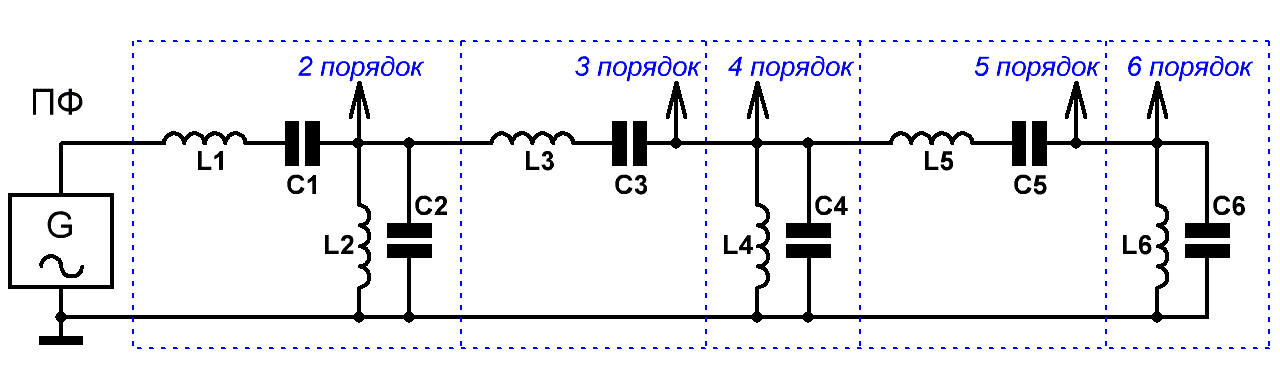

Рис.2 Схемы односторонне нагруженных LC полосовых фильтров

Разместим калькулятор расчёта элементов и для полосовых фильтров акустических систем.

КАЛЬКУЛЯТОР РАСЧЁТА ЭЛЕМЕНТОВ ПОЛОСОВЫХ LC- ФИЛЬТРОВ ДЛЯ АКУСТИКИ

При расчёте разделительных фильтров принимается допущение, что нагрузка (сопротивление динамика) — это величина чисто активная. Однако, учитывая то, что реальные громкоговорители обладают комплексным характером входного сопротивления, то для корректной работы фильтров могут потребоваться согласующие цепи, компенсирующие этот комплексный характер.
При проектировании кроссоверов — частоты среза фильтров всегда следует выбирать значительно выше резонансных частот громкоговорителей. Тогда для компенсации комплексного характера входного сопротивления громкоговорителя будет достаточно включения упрощённой согласующей цепи, называемой цепью Цобеля и представляющей собой простую цепочку из последовательно включённых сопротивления Rк и ёмкости Cк (Рис.3а).
Рэй Олден, автор одной из самых популярных книг по акустике, советует использовать следующие соотношения: R_к = 1,25*R_е ; С_к = L_е/R_е 2 , где Re и Le — это паспортные сопротивление и индуктивность динамика.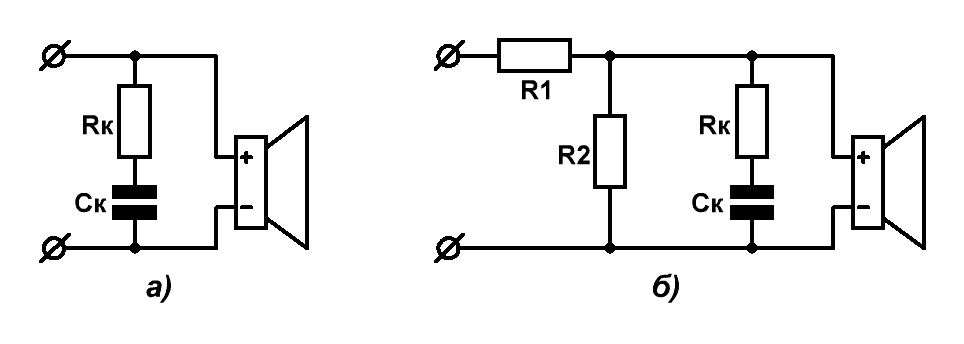

Рис.3 Согласующая цепь Цобеля и Г-образный аттенюатор для громкоговорителя

Также для уменьшения неравномерности суммарной АЧХ многополосной АС зачастую необходимо ослабить уровень каких-либо составляющих, как правило — среднечастотных либо высокочастотных. Это можно сделать с помощью Г-образных пассивных аттенюаторов, обеспечивающих заданный уровень ослабления N (дБ) (Рис.3б). Если задаться целью произвести ослабление без коррекции активного сопротивления громкоговорителя, то формулы для вычисления номиналов резисторов имеют следующий вид:
R1 ≈ R_e*(10 0,05N — 1)/10 0,05N ; R2 ≈ R_e/(10 0,05N — 1) .

Сдобрим пройденный материал калькуляторами.

КАЛЬКУЛЯТОР РАСЧЁТА ЦЕПИ ЦОБЕЛЯ ДЛЯ ГРОМКОГОВОРИТЕЛЯ

КАЛЬКУЛЯТОР РАСЧЁТА ЭЛЕМЕНТОВ АТТЕНЮАТОРА ДЛЯ ГРОМКОГОВОРИТЕЛЯ

Следует отметить, что некоторые производители акустики игнорируют согласующие цепи, считая, что компенсация комплексной характеристики портит звучание системы на реальном музыкальном материале. В таких случаях неравномерность АЧХ тракта приходится устранять при помощи измерительной аппаратуры, кропотливо подбирая каждый из элементов звеньев фильтра.
В принципе — то же самое можно сделать и на симуляторе, подставив в качестве нагрузки фильтра эквивалентную электрическую схему громкоговорителя. Естественным образом — эта схема должна учитывать акустическое оформление динамика. А как создать такую схему — мы с вами подробно обсудили на странице ссылка на страницу.

Источник

Тема: Почему Нельзя Просто Так Рассчитать Кроссовер Для Акустической Системы

Опции темы

Почему Нельзя Просто Так Рассчитать Кроссовер Для Акустической Системы

Я долго смотрел как многие «рассчитывают» фильтр, просто вбив циферки в программу и получив номиналы, принимались мотать катушки, искать кондеры и т.д.
Но это не правильно, звук от этого хуже чем у купленных каких нибудь колонок фирмы свен.

Далее текст не мой.

Допустим мы имеем две пары динамиков, пара мидбасов и пара пищалок.
Известно : их частотная характеристика (от Х до Y герц), мощность, сопротивление (Z ом) и рекомендации производителя по выборе частоты раздела/среза.
Для расчёта фильтров кроссовера нужно не много — сопротивление нагрузки(динамиков) и частоту среза. Итак мы это всё имеем в исходниках и поэтому легко рассчитываем. Получаем следующее при моделировании:

Вроде всё ровненько и красиво, но когда мы собираем рассчитанный кроссовер и подключаем его к имеющимся динамикам, то на клеммах динамиков, т.е. после кроссовера приборы нам показывают следующее:

Как же так, ведь формулы все правильные, сопротивления динамиков точные ?
Дело в том что сопротивление динамика нельзя просто выразить цифрой, допустим 4 ома, т.к. оно зависит от частоты и если на частоте 400гц оно 7 ом, то на 4000гц вполне может быть 12 ом, вот примерно так выглядит типичный график импеданса у мидбасовика

— получается кроссовер работает на не стабильную нагрузку.
Но это ещё не всё, есть ещё неравномерность АЧХ и ФЧХ головок и несовпадение их акустических центров — когда мы начинаем микрофоном замерять получившуюся АЧХ она выглядит ещё хуже

Да, это явно не то к чему мы стремились.

Текст и графики написаны, сделаны — © mAxSpace

А еще есть baffle-step http://forum.cxem.net/index.php?showtopic=70735 который подпортит еще будущую систему если его не компенсировать.

Миниатюры

Источник

Непростой расчет кроссоверов акустических систем

Как любителями звука обычно проектируется многополосная акустическая система ? Очень просто . Под имеющийся в наличии НЧ ( НЧ / СЧ ) динамик разрабатывается необходимого объема бокс . Ширину передней панели определяет размер НЧ ( НЧ / СЧ ) динамика , остальные динамики располагаются , исходя из эстетических соображений . Кроссовер рассчитывается также « классическим » методом – на бумаге ( или с помощью небольших программ ) по формулам с давно известными коэффициентами для получения требуемой характеристики фильтра . Сложив все это вместе и получив какой – то результат , одни остаются им довольны , а другие начинают задаваться вопросом : почему результат не соответствует расчетам . Не обходится и без особо « продвинутых », начинающих заявлять , что все многополосные системы , мягко говоря , не стОят внимания . Действительно , каков вывод ! В прошлом я сам рассчитывал акустические оформления и кроссоверы по формулам . Расчет кроссоверов производился , опираясь на номинальное сопротивление (Z) динамиков , после чего следовала долгая процедура подгонки « на слух ». Получалось , но не ахти как . Удовлетворительно . Все дело в том , что я не учитывал целый ряд особенностей при расчете . Особенностей , которые отличают динамики от резисторов , а многополосную акустику от точечного излучателя . Сейчас мне проще , есть измерительный комплекс , с которым я научился хорошо работать , и есть CAD системы , которые позволяют промоделировать акустику , учитывая все ее тонкости . И вот при очередном знакомстве с изделием , рассчитанным по формулам и принесенном на измерения , я решил уделить повышенное внимание кроссоверу . Конструкция , как оказалось , была с несводимыми в принципе полосами , чего на первый взгляд не скажешь . Особенно , глядя на АЧХ простого и недорогого мидбаса :

Используемый кроссовер – классика . Первый порядок на мидбасе ( на изображении выше измерения проведены без кроссовера ) и первый порядок на твитер . Казалось бы , что может быть лучше , чем фильтр первого порядка ? Практически любой аудиофил скажет , что в двухполосной акустической системе сопряженные таким фильтром головки обеспечат линейную фазо частотную характеристику ( ФЧХ ) и хорошую , без колебаний и затягивания , переходную характеристику ( ПХ ). А широкий совместный диапазон излучения можно компенсировать разнесением частот раздела . К сожалению , все хорошо только в теории . На практике же первый порядок фильтра редко работает с приемлемым результатом . Я попробую внести ясность , почему так происходит . Реальных результатов измерений не привожу , только моделирование в LspCAD. Как показала практика , результаты моделирования в этой CAD системе с высокой точностью подтверждаются результатами реальных измерений .

На изображении ниже показана двухполосная система с использованием фильтров первого порядка с частотой раздела полос 2500 Гц . Кроссовер рассчитан , исходя из номинального сопротивления нагрузки для ФНЧ – 6 Ом , для ФВЧ – 4 Ома . Динамикам присвоено константное сопротивление 6 Ом (Midwoofer) и 4 Ома (Tweeter). Размер их излучающих поверхностей составляет 1 мм , а акустические центры расположены в одной точке (x = 0, y = 0, z = 0). В общем , идеальные условия работы , чего в реальной жизни не может быть . Передаточная характеристика такой системы показана на графике рядом . Остальные характеристики в данном случае также линейны .

На первый взгляд , кроссовер идеален . Но ведь и вся система здесь представлена идеальной . Исправим досадный недочет и немного приблизим ее к реальности . Добавим подходящий бокс и используем размеры излучающих поверхностей для мидвуфера – 110 мм , а для твитера – 25.4 мм . Расположение твитера будет референсной точкой с координатами x = 0, y = 0, z = 0. Мидвуфер же, расположен ниже твитера , его акустический центр смещен вниз на 130 мм и углублен на 25 мм (x = 0, y = -130, z = 25). Среди двухполосных систем с использованием 4.5 дюймового мидвуфера и 1 дюймового твитера это типичные значения расположения акустических центров .

На первом графике изображена АФЧХ системы , на втором – внеосевые АЧХ . Ожидали такого результата ? Так как акустические центры излучателей находятся на некотором расстоянии друг от друга , между ними для звуковых волн существует временная разница , следовательно можно говорить о различии их акустических фаз . Выровнять фазовую характеристику можно двумя методами : расположением акустических центров головок строго на оси ( коаксиальный излучатель ), либо фазовой коррекцией в кроссовере . Но поскольку речь идет о фильтрах первого порядка , по понятным причинам фазовая коррекция в кроссовере с ними невозможна . Поэтому идем другим путем .

Так как на изображении выше отчетливо виден сильный провал в области частоты раздела , напрашивается мысль о противоположном знаке акустических фаз излучателей в этой области . Пробуем противофазное включение , хотя это опять в разрез идет с теорией . На сей раз о синфазной работе головок при использовании фильтров первого порядка .

Теперь АЧХ находится в пределах неравномерности +/-3 дБ , хотя с ФЧХ наблюдаются явно проблемы . Зато что происходит с внеосевыми АЧХ ! А ведь это все еще « идеальные » динамики . Добавляем реальный импеданс .

С таким фильтром твитер без каких – либо преград работает в области частоты резонанса ( а она находится достаточно низко – 750 Гц ). Мидвуфер же практически без ослабления воспроизводит всю полосу частот . Смотрим , что будет , если добавить реальные АФЧХ головок .

Спрашивается : за что боролись ? Совместная работа головок обеспечивается в диапазоне 600 Гц – 8 кГц , ФЧХ имеет излом . Внеосевые АЧХ и диаграмма направленности обещают окраску звучания в широком диапазоне частот , узкую зону стереоэффекта и необходимость прослушивания такой системы строго на оси твитера . Сам твитер работает в области резонанса , а мидвуфер – за пределами поршневой зоны . Единственное , что осталось удовлетворительным – ПХ .

При широком частотном диапазоне совместной работы головок , часто пользуются разнесением частот раздела . Пробуем такой вариант . Для ФНЧ используется частота среза 1 кГц , для ФВЧ – 6 кГц .

Прежние недостатки еще больше усугубились . Теперь наблюдается большая неравномерность осевой АЧХ и худшие внеосевые АЧХ . Может , стоит попробовать высокую – 8…10 кГц – частоту раздела ? Так как мидвуфер по результатам измерений АЧХ работает до 8 кГц , можно подключить его без фильтра , а для твитера использовать фильтр первого порядка с частотой среза 10 кГц . Пробуем такой вариант .

Как видим , ослабление на частоте резонанса твитера недостаточно даже для такой высокой частоты раздела . А что происходит с внеосевыми АЧХ ? Мидвуфер работает без фильтра в широком диапазоне частот , твитер его только поддерживает вверху , а диаграмма направленности хуже , чем в любом другом случае . Мидвуфер , в силу законов физики , имеет сужение диаграммы направленности выше частоты , которая определяется размерами его излучающей поверхности . В идеальном случае , эта частота составляет c/d, где c – скорость звука в воздушной среде (345 м / с ), d – диаметр диафрагмы ( в метрах ). Для используемого в примерах мидвуфера диаметр диафрагмы составляет 110 мм , что ограничивает его использование на частотах выше 3 кГц .

Изменение внеосевых АЧХ и сужение диаграммы направленности проявляется и в комбинированных широкополосных динамиках . Для примера , ниже приведен результат измерения широкополосного динамика 4 А 28 при измерении на оси и с отклонением от оси на 45 градусов .

Как можно видеть , изменение АЧХ происходит , начиная с частоты 1500 Гц , что хорошо согласуется с вышеприведенной формулой (c/d = 1604 Гц ).

По указанной причине , расположение акустических центров излучателей в многополосной системе должно производиться так , чтобы расстояние между ними не превышало длины волны на частоте раздела .

Что можно сделать для устранения всех перечисленных недостатков при использовании тех же мидвуфера и твитера . Не сильно углубляясь в моделирование , при использовании фильтров третього порядка я получил следующую картину .

Проведя час – другой за моделированием , можно выровнять характеристики до погрешности в пару децибел , а диаграмму направленности сделать еще шире . Резонный вопрос : совпадут ли результаты моделирования с результатами реальных измерений . Предлагаю посмотреть на изображения ниже и самому ответить на этот вопрос .

Но для того , чтобы получить требуемые результаты , CAD системе необходимо « знать » о будущей АС все : размеры бокса , расположение динамиков , их АФЧХ и ИЧХ . Иначе вместо того , что можно было бы получить:

получим то , что будет:

Автор: Сирвутис Алексей Ромасович ( Lexus )

Источник