Все автомобили уаз зеленые среди автомобилей ока нет красных

Содержание

Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
Системный подход в моделировании. ГДЗ по Информатике 11 класс.
Задачи
Урок 8 Использование графов (§7. Системный подход в моделировании)
Содержание урока
Задачи с 9 по 16
Урок 8 Использование графов (§7. Системный подход в моделировании)
Содержание урока
Задачи с 9 по 16

Учитель информатики

Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.

Системный подход в моделировании. ГДЗ по Информатике 11 класс.

Информатика. 11 класс. Углубленный уровень. В 2 ч. Поляков К.Ю., Еремин Е.А.

§ 7. Системный подход в моделировании

1. Приведите примеры, когда в одной и той же ситуации люди используют разные модели. Какие из них можно считать системами?
2. Какие два типа табличных моделей вы знаете?
3. К какому типу можно отнести модель, построенную при решении задачи с путешественником? Обоснуйте ответ.
4. Какие типы диаграмм вы знаете? В каких случаях используется каждый из них?
*5. Изучите другие типы диаграмм, которые можно построить в табличных процессорах. Зачем они используются? Приведите примеры.
6. Объясните, почему любую систему, состоящую из подсистем, можно представить в виде иерархии.
7. Вспомните, что такое матрица смежности и весовая матрица графа (см. главу 1 в учебнике для 10 класса).
8. Зачем нужны сетевые модели при планировании производства?
9. Что такое семантические сети? В чем их достоинства и недостатки?
10. Что такое семантическая паутина? Можно ли её создать на основе существующих веб-страниц? Обоснуйте свой ответ.
11. Что такое выигрышная стратегия в игре?
12. Как доказать, что заданная позиция в игре является выигрышной (или проигрышной)? Как вы думаете, в каких случаях это сделать не удаётся?
13. Почему для того, чтобы доказать выигрыш какого-то игрока в заданной начальной позиции, не нужно строить полное дерево игры?

а) «Типы диаграмм»
б) «Сетевое планирование»
в) «Семантические сети»
г) «Интеллект-карты (mind maps)»
д) «Диаграммы Ганта»
е) «Использование ленты времени»

Задачи

1. В графе 9 узлов, причём каждый узел связан со всеми другими. Сколько всего связей в этой модели?

2. Система состоит из трёх подсистем по три элемента в каждой. Все элементы в каждой подсистеме связаны со всеми другими, кроме того, каждая подсистема связана со всеми другими подсистемами. Сколько всего связей в этой системе? Сравните ответы этой и предыдущей задач, сделайте выводы.

3. Постройте матрицы смежности и весовые матрицы для следующих графов.

4. Изготовление прибора «Заря-М» описывается следующей сетевой моделью (веса дуг обозначают длительность работ в днях).

Определите, через сколько дней после начала работ будет изготовлен прибор.

5. Постройте семантическую сеть на основе текста: «Кошачьи — семейство млекопитающих отряда хищных. Кроме кошек к ним относятся, например, львы и тигры. У кошачьих развиты слух и зрение. У нас дома живёт кошка Мурка. У неё рыжая шерсть».

6. Путешественник прибыл в посёлок Луковое в полночь по местному времени и увидел следующее расписание автобусов.

Определите самое раннее время, когда он может попасть в Васильево, и как ему нужно ехать.

7. Путешественник прибыл в посёлок Сычёво в 10:00 по местному времени и увидел следующее расписание автобусов.

Определите самое раннее время, когда он может попасть в посёлок Рогатое, и как ему нужно ехать.

8. Путешественник прибыл в посёлок Кунцево в полночь по местному времени и увидел следующее расписание автобусов.

Определите самое раннее время, когда он может попасть в посёлок Ручьи, и как ему нужно ехать.

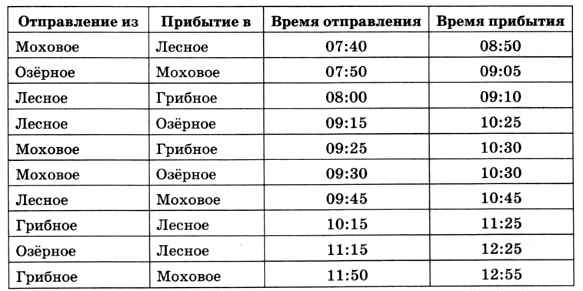
9. Путешественник прибыл в посёлок Моховое в полночь по местному времени и увидел следующее расписание автобусов.

Определите самое раннее время, когда он может попасть в посёлок Лесное, и как ему нужно ехать.

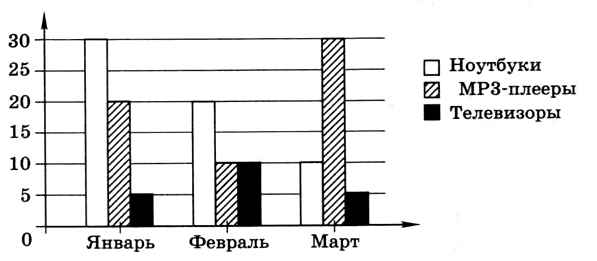
10. На диаграмме показано, сколько ноутбуков, МРЗ-плейеров и телевизоров продала некоторая фирма в первые три месяца года (I квартал).

Какая из следующих диаграмм правильно отражает соотношение общего количества проданных товаров разных видов за весь I квартал?

11. В соревнованиях участвовали спортсмены из Москвы, Санкт- Петербурга и Мурманска, каждый из них имеет III, II или I разряд. На диаграмме 1) показано количество спортсменов, имеющих разные разряды, а на диаграмме 2) — соотношение спортсменов из разных городов.

Какие из этих утверждений следуют из анализа диаграмм:

а) все спортсмены, имеющие П разряд, могут быть москвичами;
б) все спортсмены из Мурманска могут иметь II разряд;
в) все спортсмены из Санкт-Петербурга могут иметь I разряд;
г) все спортсмены III разряда могут быть из Москвы?

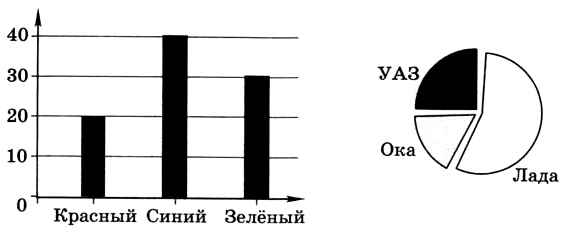
12. В салоне продаются автомашины «Лада», «УАЗ» и «Ока» трёх цветов: красного, синего и зелёного. На диаграмме 1) показано количество машин разного цвета, а на диаграмме 2) — количество машин разных марок.

Какие из этих утверждений следуют из анализа диаграмм:

а) все автомобили «УАЗ» — зелёные;
б) среди автомобилей «Ока» нет красных;
в) все автомобили «Ока» — синие;
г) среди автомобилей «Лада» есть синие?

13. Два игрока играют в следующую игру. Вначале перед ними лежит куча из некоторого количества камней (обозначим его S). За один ход игрок может добавить в кучу 2 камня или увеличить количество камней в куче в два раза. У каждого игрока есть неограниченное количество камней. Победителем считается игрок, первым получивший кучу, в которой 25 камней или больше. Для каждого значения S (1 ≤ S ≤ 24) определите, кто выиграет и за сколько ходов. Для S = 7 постройте дерево игры, показывающее стратегию выигрывающего игрока.

14. Два игрока играют в следующую игру. Вначале перед ними лежит куча из некоторого количества камней (обозначим его S). За один ход игрок может добавить в кучу 1 камень или увеличить количество камней в куче в три раза. У каждого игрока есть неограниченное количество камней. Победителем считается игрок, первым получивший кучу, в которой 55 камней или больше. Для каждого значения S (1 ≤ S ≤ 54) определите, кто выиграет и за сколько ходов. Для S = 16 постройте дерево игры, показывающее стратегию выигрывающего игрока.

15. Два игрока играют в следующую игру. Вначале перед ними лежит куча из некоторого количества камней (обозначим его S). За один ход игрок может добавить в кучу два камня, добавить в кучу три камня или увеличить количество камней в куче в два раза. У каждого игрока есть неограниченное количество камней. Победителем считается игрок, первым получивший кучу, в которой 30 камней или больше. Для каждого значения S (1 ≤ S ≤ 29) определите, кто выиграет и за сколько ходов. Для S = 9 постройте дерево игры, показывающее стратегию выигрывающего игрока.

16. Игра Баше. Два игрока играют в следующую игру. Вначале перед ними лежит куча из некоторого количества камней (обозначим его S). За один ход игрок может взять из кучи 1, 2 или 3 камня. Выигрывает тот, кто возьмет последний камень. Для каждого значения S (1 ≤ S ≤ 15) определите, кто выиграет и за сколько ходов. Для S = 12 постройте дерево игры, показывающее стратегию выигрывающего игрока.

Источник